A short article in the January issue of Physics Today
examined the physics of water jetpacks (reference below), a physics that I applied to the 1980 lateral blast at Mount St.
Helens—a scaled-up version of a jetpack!
A
water jetpack is a device that provides a platform for a person to stand on. It ejects water at high velocity to propel the person upward, for example the
Mississippi River celeb Caleb Gavic pictured above hovering over the Mississippi
River. Note, from the sketch in the picture that a fire hose feeds the jet pack, and that there are two
major thrusters and two handheld stabilizing nozzles through which water is expelled to provide the thrust to the platform. The nozzles have a
slightly smaller area (combined) than the hose that feeds the system.
Vonk
and Bohacek examine a number of scenarios for the physics of this machine, starting with a
one-dimensional, steady state model in which they ask simply "how much thrust does it take to support the weight of the pilot and his platform?" That weight for
Gavic and his platform is 10 Newtons (N). Using F=dp/dt (F=force=thrust,
p=pressure, t=time)--Newton’s second law--this force must be equal to the
change in momentum per unit time of the water stream at the platform. The
change of momentum is proportional to the difference (per unit time) between
the velocity of the water approaching the platform (v1) and the water being expelled
at the platform (v2). That is, F = (dm/dt)(v2-v1).
From
conservation of energy, the mass change, dm/dt, is dm/dt=rho*v2*(2At+TAs), where
rho is the density of the water, and At and As are, respectively the
cross-sectional areas of the thrusters and the stabilizers. Assuming no loss of
water (i.e., no leaks), this must be equal to the mass (or volume since this is
incompressible flow) of water approaching through the hose. Setting these two
quantities equal to each other, and manipulating, gives v1=-v2(2At + 2As)/Ah,
where Ah is the cross-sectional area of the feeding hose. The minus sign arises
because the approach and exit velocities are approximately in opposite
directions.
When substituted into the equation for force (above), this yields
an expression too cumbersome to type on a blog, but a relatively simple
expression for the force that depends on five quantities: rho, v1, At, As, Ah. Plugging in
the known values and solving for the velocity of the water ejected by the
thrusters, v2,
they calculated a velocity of 10 m/s, about 23 mph.
When
compared to a velocity that they could estimate from tracking knots of water in
a video of the jetpack, they found that the actual speed was 15 m/s, in the
ballpark of the 23 mph calculated but only in the ballpark. To get a more accurate answer, they refined
the model to take account of the fact that the hose is pulled down by gravity with a force equal to its weight and the water within it, and the fact
that there is tension in the hose. They also considered that there is a
deflection of the thrusters in the horizontal direction (see photo). With these refinements,
they got the model to be within about 15% of the measured quantities. Estimates of the ejected water speed range between roughly 10 and 20 m/s with the different models.The thrust is in the range of 1660 N.
For comparison, one of the most impressive displays
of power created by humans was the launching of a Saturn 5 rocket that carried
Apollo astronauts to the moon. The first stage of the Advanced Saturn 5
consisted of five F-1 liquid-oxygen/kerosene motors. The thrust of the Saturn 5 rockets that propelled Americans to the moon was 7.5 million pounds (3.3 x 10^7 N), about 20,000 times as great as the water jetpacks!
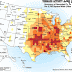
In 1980 when I worked at Mount St. Helens after the lateral blast of May 18, I proposed that the blast resembled the discharge of a giant rocket nozzle, where the "propellent" was the hot gas inside the volcano that was released when exposed by a giant landslide. An area of over 500 square kilometers (the white area in the sketch) was decimated. I calculated the thrust using the same principles as above for the water jetpack (reference is Kieffer below). Two factors contributed to the thrust of the blast being much larger than that of either the jetpacks or the Saturn V: the enormous area of the vent and the heavy mass loading of the gas.
The mass flux area at the
exit of an F-1 motor was about 25 g/s/cm^2;
that of the lateral
blast at the Mount St. Helens vent was 240 times as great (these calculations are in the Kieffer reference below). The power per unit
area of the F-l motors was approximately 0.8 Mwatt/cm^2; that of the lateral
blast was three times greater. The Saturn 5 power was delivered over five
rockets covering roughly 50 m^2; the blast at Mount St. Helens flowed out of a
vent more than 2,000 times this area. The total power of the five Saturn 5
motors was about 4 x 10^5 megawatts;
that of the blast was nearly 16,000 times as great. The thrust of the Saturn 5
was 7.5 million pounds (3.3 x 10^7 N);
that of the blast was 10^5 greater. (This calculated number was almost identical
to the thrust estimated from seismic measurements of the blast, see Kanamori and Given reference below.)
The lateral
blast of May 18 was indeed an awesome event by both human and geologic standards, and certainly dwarfed that of the water jet pack!
Vonk, Matthew and Bohacek, Peter, “Carried by Impulse: The physics of water jetpacks,” Physics Today, p. 54-55, January 2013)
Kieffer, S. W., "The blast at Mount St. Helens: what happened?" Engineering and Science, 45(1), 6-12, 1981.
Kanamori, Hiroo and Given, Jeffrey W., "Analysis of long-period seismic waves excited by the May 18, 1980, eruption of Mount St. Helens-a terrestrial monopole?" Journal of Geophysical Research, 87(B7), 5422-5432, 1982.












1 comment:
Sue-
Someone put the slides in the projector backwards!
(all the illustrations on your posts are mirror-image)
Michael Tiffany
Post a Comment